NRA CET Exam 2021 Information:
- Computer Based Preliminary Exam
- Score Card valid for 3 years
- Exam centre in every District for candidates
- Jobs in PSU, Private companies and State Government based on CET Score
- Different syllabus for each level in NRA CET
- Candidates must be citizen of India
- Practicing with Online Test Series will enhance your overall performance
- Practice more and more questions will help you to score better and understand the question
- Accuracy is the key and to avoid the reduction in marks in exam practice these quizzes and
- In order to finish the section on time, you need time and management both.
- Most important is to avoid anxiety and by practice you will experience real time scenario.
- Arithmetic Section in NRA CET 2021 consists of following syllabus, one must be familiar with the pattern and the type of Topics asked in the section.
Compound Interest
It is based on initial principle and the accumulated interest from previous periods. The rate at which compound interest accrues depends upon the frequency of compounding, such that the higher the number of compounding periods, the greater the compound interest.
Compound Interest Questions for NRA CET 10th (Matriculate) Level:
Ex.
Rahul took a loan of Rs. 36000 at 20% compound interest, the interest being compounded annually. He repaid some amount at the end of the first year and then paid Rs. 28800 at the end of the second year and cleared the loan. The amount he paid at the end of the first year was.
Rs. 18400
Rs. 19200
Rs. 24400
Rs. 28200
Solution :
Compound Interest Questions for NRA CET 10th (Matriculate) Level:
Ex.
Rahul took a loan of Rs. 36000 at 20% compound interest, the interest being compounded annually. He repaid some amount at the end of the first year and then paid Rs. 28800 at the end of the second year and cleared the loan. The amount he paid at the end of the first year was.
Rs. 18400
Rs. 19200
Rs. 24400
Rs. 28200
Solution :
Let the amount he paid at the end of the first year be x
Value of 36000 at the end of 1st year = 43200
The amount to be paid at the end of second year in order to clear the loan
| = (43200 – x) + | 20 | × (43200 – x) |
| 100 |
Or, 1.2(43200 – x) = 28800
Or, x = 19200
Hence, option (B) is correct.
Hence, option (B) is correct.
Compound Interest Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Shivani has some amount of money ans she invested the money in two schemes A and B in the ratio of 2 : 5 for 2 years, scheme A offers 30% pa compound interest and scheme B offers 15% pa Simple interest. Difference between the interest earned from both the schemes is Rs.1080. How much was invested in scheme B?
Rs. 45000
Rs. 36000
Rs. 40000
Rs. 50000
Solution :
Let the amount invested in scheme A is 2 × 50 = 100, the amount invested in scheme B is 5 × 50 = 250
| Interest from scheme A = 100 × | ( | 1 + | 30 | ) | 2 |
| 100 |
= 169 – 100 = Rs.69
Interest from scheme B = 250 × 15% × 2
= Rs.75
Difference between interest = 75 – 69 = Rs.6
If the difference is Rs.6., investment in scheme B = Rs.250
so the difference is Rs.1080 .,
| investment in scheme B =Rs. | 250 | × 1080. = Rs.45000 |
| 6 |
Hence, option A is correct.
Compound Interest Questions for NRA CET Graduate Level:
Ex.
Aman gives Rs. 500000 to Bhuvan at 12% p.a. compound interest for two years. Bhuvan gives 80% of the money received from Aman to Chetan at 20% p.a. interest, compounded half yearly for two years. Two years later he receives his due amount from Chetan and gives Aman his due amount. What is the amount left with Bhuvan?
Rs. 52980
Rs. 58440
Rs. 67880
Rs. 62780
Solution :
Money Bhuvan has to return to Aman after two years
| = 500000 × | ( | 1 + | 12 | ) | 2 | = Rs. 627200 |
| 100 |
Money given by Bhuvan to Chetan = 80% (500000) = Rs. 400000, so amount left with him = Rs. 100000
Amount Chetan returns to Bhuvan after two years
| = 400000 × | ( | 1 + | 10 | ) | 4 | = Rs. 585640 |
| 100 |
Total amount after receiving money from Chetan after two years = Rs. (585640 + 100000) = Rs. 685640
Money left after returning due amount of Aman = Rs. (685640 – 627200) = Rs. 58440
Hence, option B is correct.
Data Interpretation
It is the data which requires analysing to arrive at a inference. It requires findings, conclusions, recommendations. It is a method used to derive useful information from a collected set of data. The collected data could be in the form of Pie chart, graph tables etc. The data has to be analysed and utilised by the student to write providing the factual information.
Data Interpretation Questions for NRA CET 10th (Matriculare) Level :
Directions (1 to 3) : Study the following line chart carefully and answer the question given beside.
Data Interpretation Questions for NRA CET 10th (Matriculare) Level :
Directions (1 to 3) : Study the following line chart carefully and answer the question given beside.
Net profit (in lakhs) of three companies is compared over the different years
.png) |
Ex. 1
Find the ratio of profit of all the three companies - Maruti, Tata and Honda respectively in the year 2005.
Find the ratio of profit of all the three companies - Maruti, Tata and Honda respectively in the year 2005.
(A.) 3 : 8 : 10
(B.) 5 : 8 : 10
(C.) 1 : 3 : 7
(D.) 5 : 8 : 11
Solution :
Solution :
Profit of Maruti in the year 2005 = 25 lacs
Profit of Tata in the year 2005 = 40 lacs
Profit of Honda in the year 2005 = 50 lacs
Ratio = 25 : 40 : 50 = 5 : 8 : 10
Option B, is hence the correct answer.
Ex.2
Find the percentage change in the profit of Tata form year 2000 to 2015?
Ex.2
Find the percentage change in the profit of Tata form year 2000 to 2015?
(A.) Profit is decreased by 15 %
(B.) Profit is decreased by 20%
(C.) Profit is decreased by 30%
(D.) Profit remains same.
Solution :
Profit of Tata in the year 2000 = 50
Profit of Tata in the year 2015 = 40
Percentage change in profit
= – 20%
So, the profit is decreased by 20%.
Option B, is hence the correct answer.
Ex. 3
Find the sum of the profit of Maruti and Honda in the year 2005 and profit of Tata in the year 2015 together.
Solution :
Total wasted amount of Iron ore mined by machines A, C and E together = (20 + 8 + 28)% of 25 kg = 14 kg
Total amount of Iron extracted from the Iron ore mined by machines A, C and E together = 105 – 14 = 91 kg.
Hence, option A is correct.
Ex. 2
Total wasted amount of Iron ore mined by machine E = 28% of 25 = 7 kg
Amount of Iron extracted from Iron ore at present = 50 – 7 = 43 kg
Amount of Iron extracted from Iron ore at the end of 2 years from present = 90% of 90% of 43 = 34.83 kg
Total cost of Iron extracted from Iron ore mined by machine E = 34.83 × 200 = Rs.6966
Hence, option C is correct.
Ex. 3
Solution :
Total amount of Iron ore mined by machine B
Total cost of Iron ore mined by machine B = 40 × 200 = 8000
Total wasted amount of Iron ore mined by machine B = 16% of 25 = 4 kg
Amount of Iron extracted from Iron ore = 40 – 4 = 36 kg
Total cost of Iron extracted from Iron ore by machine B = 36 × 250 = 9000
Hence, option B is correct.
Simplification Questions for NRA CET Graduate Level:
Ex.
112 + 83 + (3125)1/5 = ? + 7
631
656
684
712
Solution :
C's new net investment = 6x – 2x = 4x
Ratio of profit : (6× x + 3x × 6): (4x × 6 + 8x × 6) :(6x × 6 + 4x × 4)
= 24x : 72x : 60 x
= 2 : 6 : 5
Hence, option B is correct answer.
Partnership Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Partnership Questions for NRA CET Graduate Level :
Ex.
The initial investments of three persons, Seeta, Geeta, and Meeta was in the ratio of 4 : 6 : 9 respectively. At the end of one – year, they divided the profit in the ratio of 4: 5: 6 respectively. If Seeta had invested for exactly 12 months then Meeta’s investments was how many months more/less thant that of Geeta’s investments?
Hence, option (A) is correct.
Boat and Stream Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Amit goes Mumbai to Kolkata by sea route. The speed of the boat in still water is 60 km/h and speed of the current is 15 km/h. After reaching Kolkata he stayed there for 20 minutes and after that come back by same boat. The time taken by him in this journey is 19 hours 32 minutes, find the distance travel by him in one side.
450 km
360 km
540 km
600 km
Solution:
Time taken by him in travelling = 19 hours 32 minutes – 20 minutes
= 19 hours 12 minutes
Let Distance = x km
According to the question,
x = 540 km
Hence, option C is correct.
Boat and Stream Questions for NRA CET Graduate Level :
Ex.
The speed of current is 5 km/h. What will be the respective downstream speed and upstream speed of a boy rowing a boat, if one third of the distance covered going downstream in a certain time is equal to the distance covered going upstream in the same time.
⇒ X + 5 = 3X – 15
⇒ 2X = 20
⇒ X = 10 km/h
Downstream speed = 10 + 5 = 15 km/h
Upstream speed = 10 – 5 = 5 km/h
Hence, option A is correct.
Hence, option (C) is correct.
Ex.
In a school number of students in 6th and 7th class is in the ratio 6 : 11. If 60% of total students in class 6 are boys and 52% of total students in class 7 are boys, then find total girls in both the class together is approximately what percentage of total students in both the classes?
So total girls = 2.4x + 5.28x = 7.68x
Hence, option B is correct.
Solution :
Let initial quantites of P and Q be 4x & x.
In 10 litres of mixture, quantity of liquid P = 4/5 x 10 = 8, therefore quantity of liquid Q = 2
When 10 litres of mixture taken out & 10 litres liquid Q is added, we get
⇒ 12x – 24 = 2x + 16
⇒ 10x = 24 + 16
So, the initial quantity of liquid Q was = 1x = 4 litres
Hence, option C is correct
⇒ 300 + 5a = 200 + 10a
⇒ 5a = 100
⇒ a = 20
Hence, option (D) is correct.
Ex.
A milkman completely fills his 24 liter cistern with two type of milks A and B in the ratio 7 : 5. The cost price of type A milk is Rs.45 per liter. If he sold this mixture at the rate of Rs.56 per liter at a profit of 12%, then find the per liter cost price of type B milk.
Solution :
SP of mixture = 24 × 56 = Rs.1344
CP of mixture when sold at 12% profit
CP of type A milk = 14 × 45 = Rs.630
CP of type B milk = Rs. (1200 – 630) = Rs.570
Hence, option D is correct.
The time taken to cover the remaining distance 2x km=
Quantity I: the average speed in meter per sec
Quantity II: 12.5 meter per sec
Therefore, Q1 < Q2
Hence, option C is correct.
Let length = l cm then breadth = (l – 3.3) cm
We know that, in a rectangle, diagonal2 = l2 + b2
16.5 = (l2 + (l – 3.3)2
272.25 = l2 + (l – 3.3)2
By solving, l = 13.2 cm
b = (13.2 – 3.3) = 9.9 cm
Area = l × b = 13.2 × 9.9 = 130.68 sq. cm
Quantity II : 125 sq. cm
Therefore, Quantity : I > Quantity : II
Hence, option A is correct.
Hence, option D is correct.
Hence, option (D) is correct.
Ex.
1, 5, 19, 81, ?, 2473
814
389
675
411
Solution :
Hence, option (D) is correct.
So, According to given condition :-
⇒ 200 R = 10,000
R = 50%
Hence, option (D) is correct.
Solution:
Let the principal = Rs. 100x
Then, according to the question, SI = 2 × 100x = 200x
R = 20%
The CI on Rs. 100x for 2 years
The required ratio = 100x : 44x = 25 : 11
Hence, option C is correct.
Ex.
From a bank, Ram and Shyam together took a certain amount under simple interest and they lent the total amount to Mohan at 2% more simple interest. At the end of 4 years, the total money earned by Ram after paying the interest to the bank was Rs. 400 more than that of Shyam. From the bank, the total amount taken by Ram was how much more than that of Shyam?
Solution :
Let Ram took Rs. a and Shyam took Rs. b
Let the rate of interest was r% per annum
They lent Rs. (a + b) to Mohan at the rate of (r + 2)% per annum
For Ram,
The total interest earned by Ram after paying the interest to the bank
For Shyam,
The total interest earned by Ram after paying the interest to the bank
From the question,
a – b = 50 × 100 = Rs. 5000
Hence, option C is correct.
Therefore discount = 29000 – 26680 = Rs 2320
Discount percent = d
d = 8%
Hence, option (B) is correct.
Since shopkeeper has to gain this amount by selling remaining 45 dozen of bottles
Hence, option (C) is correct.
SP to gain Rs.900 = Rs. (37500 + 900) = Rs. 38400
New Discount = Rs. (40000 – 38400) = Rs. 1600
Hence, option E is correct.
Solution :
Solution :
At present, five times of the age of Rahul is equal to three times of the age of Rocky
Rahul’s age: Rocky’s age = 3 : 5
Let the age of Rahul = 3x years then the age of Rocky = 5x years
The age of Rocky’s wife = 5x – 5 years,
5 years ago, the age of Rahul = 3x – 5 years
The age of Rocky’s wife = 5x – 5 – 5 years
9x – 15 = 10x – 20
x = 5 years
At present, the sum of their age = 3x + 5x + 5x – 5 years = 13x – 5 = 65 – 5 = 60 years
Hence, option C is correct.
Solution :
Hence, option D is correct.
Hence, option (C) is correct.
240
560
720
360
Ex.
How many 3 - letter words with or without meaning, can be formed out of the letters of the word, 'LOGARITHMS', if repetition of letters is not allowed?
720
420
5040
120
Solution :
Ex.
Five people out of whom only two can drive are to be seated in a five seater car with two seats in front and three in the rear. The people who know driving don’t sit together. Only someone who knows driving can sit on the driver’s seat. Find the number of ways the five people can be seated.
Solution :
Hence, option D is correct.
200m
115m
225m
150m
Solution :
If two trains are going towards each other, then their relative speed = Summation of their speeds
Now we can write,
⇒ 2x = 400
⇒ x = 200
12 seconds
10 seconds
13 seconds
9 seconds
Solution :
Let, length of the platform = x m
And, length of the Toofan express = y m
So, 380 + x = 1110
x = 1110 – 380 = 730
= y + 730 = 1065
= y =1065 – 730 = 335 m
Hence, option C is correct.
Ex.
Ajay walked 12 km to reach the station from his house. Then he boarded in a train and reached his destination. The average speed of the entire journey was 62 kmph and he took a total time of 6 hours. If the average speed of train was 120 kmph, then what is the ratio of walking speed of Ajay to the speed of train?
Required ratio = 4 : 120 = 1 : 30
Hence, option A is correct.
56
36
26
16
34
Solution :
A can do a piece of work in 4 hours. B and C can do it in 3 hours. A and C can do it in 2 hours. How long will B alone take to do it?
10 hours
12 hours
8 hours
24 hours
Solution :
(A + B + C) 's one hour's work = 1/4 + 1/3 = 7/12
Hence, B alone con do the work in 12 hours.
Hence, option B is correct.
Hence, C can complete the work alone in 24 days.
Hence, option (C) is correct.
Hence, option A is correct.
Solution :
49
89
92
96
None of these
Solution :
Let the number of non-officers in office = x
Now, according to question-
⇒ 400x + 1040 × 30 = 500(30 + x)
⇒ 400x + 1040 × 30 = 500 × 30 + 500x
⇒ 100x = 30 (1040 – 500)
⇒ 100x = 30(540)
⇒ x = 162
Hence, option D is correct.
on comparing the values of x and y, we get
Hence, either x = y or relationship cannot be established.
Solution :
Profit of Tata in the year 2000 = 50
Profit of Tata in the year 2015 = 40
Percentage change in profit
| 40 – 50 | × 100 |
|
50
|
= – 20%
So, the profit is decreased by 20%.
Option B, is hence the correct answer.
Ex. 3
Find the sum of the profit of Maruti and Honda in the year 2005 and profit of Tata in the year 2015 together.
(A.) 105 lacs
(B.) 110 lacs
(C.) 120 lacs
(D.) 115 lacs
Solution :
Profit of Maruti in the year 2005 = 25
Profit of Honda in the year 2005 = 50
Profit of Tata in the year 2015 = 40
Sum of the profits of Maruti and Honda of the year 2005 and profit of Tata in the year 2015 = (25 + 50) + 40 = 75 + 40 = 115
Option D, is hence the correct answer.
Data Interpretation Questions for NRA CET 12th (Higher Secondary) Level:
Directions (1 to 3) : Study the following table chart carefully and answer the question given beside.
Data Interpretation Questions for NRA CET 12th (Higher Secondary) Level:
Directions (1 to 3) : Study the following table chart carefully and answer the question given beside.
The following table represents the number of items sold by five different stores in six different days of a week.
Ex. 1
Number of items sold by A on Tuesday is what percent more than the number of items sold by C on Sunday?
Number of items sold by E on Friday = 1400
Hence, option (D) is correct.
Data Interpretation Questions for NRA CET Graduate Level:
| Stores | Sunday | Monday | Tuesday | Wednesday | Thursday | Friday |
| A | 3500 | 2200 | 2600 | 2800 | 2200 | 2500 |
| B | 1800 | 1600 | 3200 | 1500 | 2800 | 2600 |
| C | 2400 | 2800 | 2000 | 1400 | 1800 | 1800 |
| D | 1700 | 3000 | 1800 | 2000 | 1000 | 2000 |
| E | 2000 | 2500 | 1600 | 1400 | 3400 | 1400 |
Ex. 1
Number of items sold by A on Tuesday is what percent more than the number of items sold by C on Sunday?
(A.) 5.33%
(B.) 8.33%
(C.) 6.33%
(D.) 7.33%
(E.) None of these
Solution :
Number of items sold by A on Tuesday = 2600
Number of items sold by C on Sunday = 2400
Hence, option (B) is correct.
Ex.2
Find the sum of total number of items sold by store B on all the days and total number of items sold by store D on all the days.
Solution :
Number of items sold by A on Tuesday = 2600
Number of items sold by C on Sunday = 2400
| Reqd. % = | 2600 – 2400 | × 100 = 8.33% |
| 2400 |
Hence, option (B) is correct.
Ex.2
Find the sum of total number of items sold by store B on all the days and total number of items sold by store D on all the days.
(A.) 25000
(B.) 15000
(C.) 35000
(D.) 20000
(E.) None of these
Solution :
Number of items sold by C on Thursday = 1800Solution :
Total number of items sold by store B on all the days = 1800 + 1600 + 3200 + 1500 + 2800 + 2600 = 13500
Total number of items sold by store D on all the days = 1700 + 3000 + 1800 + 2000 + 1000 + 2000 = 11500
Required sum = 13500 + 11500 = 25000
Hence, option (A) is correct.
Ex. 3
Number of items sold by C on Thursday is what percent of the number of items sold by E on Friday?
Ex. 3
Number of items sold by C on Thursday is what percent of the number of items sold by E on Friday?
(A.) 108.75%
(B.) 138.56%
(C.) 118.75%
(D.) 128.57%
(E.) None of these
Solution :
Solution :
Number of items sold by E on Friday = 1400
| Reqd. % = | 1800 | × 100 = 128.57% |
| 1400 |
Hence, option (D) is correct.
Data Interpretation Questions for NRA CET Graduate Level:
Directions (1 to 3) : Study the following pie charts carefully and answer the question given beside.
Given pie chart shows the part of iron ore mined by 6 different machines in a day.
Total amount of iron ore that is mined in a day by 6 machines is 200 kg.
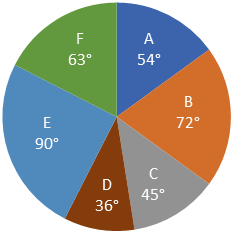 |
Given pie chart shows the wasted per cent of iron ore which is mined by 6 different machines in a day while extracting Iron from them.
Total amount of wasted iron ore in a day which is mined by 6 machines together is 25 kg.
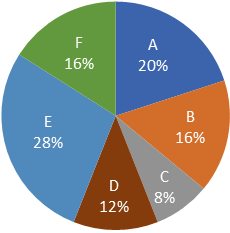 |
Amount of mined Iron ore = Extracted amount of Iron + Wasted amount of Iron ore.
Ex. 1
What is the total amount of Iron extracted from the Iron ore mined by machines A, C and E together?
What is the total amount of Iron extracted from the Iron ore mined by machines A, C and E together?
(A.) 91 kg
(B.) 96 kg
(C.) 101 kg
(D.) 106 kg
(E.) 86 kg
Solution :
Total amount of Iron ore mined by machines A, C and E together
Solution :
Total amount of Iron ore mined by machines A, C and E together
| = 200 × | 54 + 45 + 90 | = 105 kg |
| 360 |
Total wasted amount of Iron ore mined by machines A, C and E together = (20 + 8 + 28)% of 25 kg = 14 kg
Total amount of Iron extracted from the Iron ore mined by machines A, C and E together = 105 – 14 = 91 kg.
Hence, option A is correct.
Ex. 2
Due to rusting the amount of Iron extracted from Iron ore mined by machine E is decreased by 10% every year. Find the cost price of Iron extracted from Iron ore mined by machine E at the end of 2 years from now. Cost of Iron is Rs.200 per kg at present and remains same in future.
(A.) Rs. 8600
(B.) Rs. 7960
(C.) Rs. 6966
(D.) Rs. 9666
(E.) None of these
Solution :
Total amount of Iron ore mined by machine E
Solution :
Total amount of Iron ore mined by machine E
| = 200 × | 90 | = 50 kg |
| 360 |
Total wasted amount of Iron ore mined by machine E = 28% of 25 = 7 kg
Amount of Iron extracted from Iron ore at present = 50 – 7 = 43 kg
Amount of Iron extracted from Iron ore at the end of 2 years from present = 90% of 90% of 43 = 34.83 kg
Total cost of Iron extracted from Iron ore mined by machine E = 34.83 × 200 = Rs.6966
Hence, option C is correct.
Ex. 3
Cost of Iron ore after mining is Rs.200 per kg and cost of Iron after extracting from Iron ore is Rs.250 per kg, then find the per cent profit of a person if he sold the Iron extracted from Iron ore mined by machine B instead of Iron ore mined by machine B itself.
(A.) 7.5%
(B.) 12.5%
(C.) 18.5%
(D.) 15%
(E.) None of these
(D.) 15%
(E.) None of these
Solution :
Total amount of Iron ore mined by machine B
| = 200 × | 72 | = 40 kg |
| 360 |
Total cost of Iron ore mined by machine B = 40 × 200 = 8000
Total wasted amount of Iron ore mined by machine B = 16% of 25 = 4 kg
Amount of Iron extracted from Iron ore = 40 – 4 = 36 kg
Total cost of Iron extracted from Iron ore by machine B = 36 × 250 = 9000
| Profit % = | 9000 – 8000 | × 100 = 12.5% |
| 8000 |
Hence, option B is correct.
Simplification
It is the simplest questions in exam, it checks the analytical thinking of an individual. It generally means to find an answer for the complex calculation that may involve numbers on division, multiplication, square roots, cube roots, plus and minus.
Simplification is asked in the exam to check the ability of an aspirant to deal with numbers which can be of the following two types:
Sometimes, calculation is given and one of the numbers is missing from the calculation. To find out the missing number we have to approximate the given numbers.
Sometimes all the numbers are given with some operations between them and we have to simplify the calculation.
Simplification Questions for NRA CET 10th (Matriculate) Level:
Ex.
What is the remainder when we divide 390 + 590 by 34?
0
17
33
1
Solution :
Simplification is asked in the exam to check the ability of an aspirant to deal with numbers which can be of the following two types:
Sometimes, calculation is given and one of the numbers is missing from the calculation. To find out the missing number we have to approximate the given numbers.
Sometimes all the numbers are given with some operations between them and we have to simplify the calculation.
Simplification Questions for NRA CET 10th (Matriculate) Level:
Ex.
What is the remainder when we divide 390 + 590 by 34?
0
17
33
1
Solution :
390 + 590 can be written as (32)45 + (52)45
= (9)45 + (25)45
Any number of the form an + bn is a multiple of (a + b), whenever n is odd.
So (9)45 + (25)45 is a multiple of 9 + 25 = 34
So, the remainder when we divide 390 + 590 by 34 is equal to 0.
Hence, option (A) is correct.
Simplification Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
45% of 150 – 65% of 250 = ? – 56
– 49
49
– 39
39
Solution :
Simplification Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
45% of 150 – 65% of 250 = ? – 56
– 49
49
– 39
39
Solution :
45% of 150 – 65% of 250 = ? – 56
⇒ 67.5 – 162.5 + 56 = ?
⇒ 123.5 – 162.5 = ?
⇒ – 39
Hence, option C is correct.
Simplification Questions for NRA CET Graduate Level:
Ex.
112 + 83 + (3125)1/5 = ? + 7
631
656
684
712
Solution :
112 + 83 + (3125)1/5 = ? + 7
? = 121 + 512 + 5 – 7
? = 631
Hence, option A is correct.
Partnership
It helps two people to co-own a business or organisation and they decide to share the profit and loss together. It’s an arrangement where parties known as business partners, agree to cooperate to advance their mutual interest. The partners in a partnership may be individuals, business, interest based organisations, schools, government or combinations. Organisations may partner to increase the likelihood of each achieving the mission and to amplify their reach.
Partnership Questions for NRA CET 10th (Matriculate) Level:
Ex.
A, B, C started a business with their investment in ratio 1 : 4 : 6. After 6 months A invested double the money as before and B invested same amount again whereas C withdrew 1/3 rd part of his investment. Find the ratio of their profit at the end.
2 : 3 : 5
2 : 6 : 5
3 : 6 : 1
3 : 6 : 5
Solution :
Let A ,B and C invested x, 4x and 6x amount of money respectively.
After 6 months :-
A invested = 2x
A's new net investment = 2x + x = 3x
B invested = 4x
B's new net investment = 4x + 4x = 8x
Partnership Questions for NRA CET 10th (Matriculate) Level:
Ex.
A, B, C started a business with their investment in ratio 1 : 4 : 6. After 6 months A invested double the money as before and B invested same amount again whereas C withdrew 1/3 rd part of his investment. Find the ratio of their profit at the end.
2 : 3 : 5
2 : 6 : 5
3 : 6 : 1
3 : 6 : 5
Solution :
Let A ,B and C invested x, 4x and 6x amount of money respectively.
After 6 months :-
A invested = 2x
A's new net investment = 2x + x = 3x
B invested = 4x
B's new net investment = 4x + 4x = 8x
| C withdraw = | 1 | × 6x = 2x |
| 3 |
C's new net investment = 6x – 2x = 4x
Ratio of profit : (6× x + 3x × 6): (4x × 6 + 8x × 6) :(6x × 6 + 4x × 4)
= 24x : 72x : 60 x
= 2 : 6 : 5
Hence, option B is correct answer.
Partnership Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Satyam invested Rs. 2250 in a business and after some time Sundar also join him and invested Rs. 2500. At the end of year Sundar received Rs. 2750 profit out of Rs. 6050. After how much time did he join the business?
9
6
4
None of these
Solution :
9
6
4
None of these
Solution :
Satyam's Profit = 6050 - 2750 = Rs. 3300
Sundar's profit = Rs. 2750
Ratio of the profit = 3300 : 2750 = 6 : 5
Because the ratio of the capital is equals to the ratio of the profit then,
2250 × 12 : 2500 × x = 6 : 5
5 ( 2250 × 12) = 6 ( 2500 × x)
x = 9 months
So Sundar invested after 3 months.
Hence, option D is correct.
Partnership Questions for NRA CET Graduate Level :
Ex.
The initial investments of three persons, Seeta, Geeta, and Meeta was in the ratio of 4 : 6 : 9 respectively. At the end of one – year, they divided the profit in the ratio of 4: 5: 6 respectively. If Seeta had invested for exactly 12 months then Meeta’s investments was how many months more/less thant that of Geeta’s investments?
2 months less
3 months less
2 months more
3 months more
Solution :
Solution :
The ratio of their investments = 4 : 6 : 9
Let Geeta had invested for x months and Meeta’s investments = y months
Then, at the end of 1 year, the ratio of profit = 4 × 12 : 6 × x : 9 × y = 4 : 6 : 9
4 × 12 : 6 × x = 4: 5
By solving, x = 10 months
4 × 12 : 9 × y = 4 : 6
By solving, y = 8 months
y = x – 2 years
Therefore, Meeta’s investments was 2 months less than that of Geeta’s investments
Hence, option A is correct.
Boats and Streams
The direction of the boat against the stream is upstream. The direction of the boat along the stream is downstream.
Types of Question asked
Time Based Questions – The time taken by a boat to travel upstream or downstream may be asked with the speed of a boat in still water and speed of the stream given in the question.
Speed Based Questions – Questions to ask the speed of the or the speed of the boat in still water may be asked
Questions on Average Speed – With the speed of the boat upstream and downstream given in the question, the average speed of the boat may be asked.
Question Based on distance – The distance travelled by boat upstream or downstream may be asked
Boat and Stream Question for NRA CET 10th (Matriculate) Level:
Ex.
A boat rows 60 km upstream in 12 hours and a distance of 56 km in 8 hours in downstream, then the speed of stream is:
1 km/hr
2 km/hr
3 km/hr
4 km/hr
Solution :
Types of Question asked
Time Based Questions – The time taken by a boat to travel upstream or downstream may be asked with the speed of a boat in still water and speed of the stream given in the question.
Speed Based Questions – Questions to ask the speed of the or the speed of the boat in still water may be asked
Questions on Average Speed – With the speed of the boat upstream and downstream given in the question, the average speed of the boat may be asked.
Question Based on distance – The distance travelled by boat upstream or downstream may be asked
Boat and Stream Question for NRA CET 10th (Matriculate) Level:
Ex.
A boat rows 60 km upstream in 12 hours and a distance of 56 km in 8 hours in downstream, then the speed of stream is:
1 km/hr
2 km/hr
3 km/hr
4 km/hr
Solution :
| Speed of boat in upstream = | 60 | = 5 Kmph |
| 12 |
| Speed of boat in downstream = | 56 | = 7 Kmph |
| 8 |
| Speed of stream = | 1 | (speed in downstream – speed in upstream) |
| 2 |
| = | 1 | (7 – 5) = 1 km/hour |
| 2 |
Hence, option (A) is correct.
Boat and Stream Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Amit goes Mumbai to Kolkata by sea route. The speed of the boat in still water is 60 km/h and speed of the current is 15 km/h. After reaching Kolkata he stayed there for 20 minutes and after that come back by same boat. The time taken by him in this journey is 19 hours 32 minutes, find the distance travel by him in one side.
450 km
360 km
540 km
600 km
Solution:
Time taken by him in travelling = 19 hours 32 minutes – 20 minutes
= 19 hours 12 minutes
Let Distance = x km
According to the question,
| x | + | x | = 19 | 12 |
| 60+15 | 60 – 15 | 60 |
| x | + | x | = | 96 |
| 75 | 45 | 5 |
| 5x + 3x | = | 96 |
| 225 | 5 |
| 8x | = | 96 |
| 225 | 5 |
x = 540 km
Hence, option C is correct.
Boat and Stream Questions for NRA CET Graduate Level :
Ex.
The speed of current is 5 km/h. What will be the respective downstream speed and upstream speed of a boy rowing a boat, if one third of the distance covered going downstream in a certain time is equal to the distance covered going upstream in the same time.
15 kmph, 5 kmph
20 kmph, 10kmph
18 kmph, 8 kmph
24 kmph, 14 kmph
Solution :
Let the speed of boy in still water be X km/h
And the speed of current is given = 5 km/h
Downstream speed = (X + 5) km/h
Upstream speed = (X – 5) km/h
Let time be ‘t’ hours.
Solution :
Let the speed of boy in still water be X km/h
And the speed of current is given = 5 km/h
Downstream speed = (X + 5) km/h
Upstream speed = (X – 5) km/h
Let time be ‘t’ hours.
| ⇒ | (X + 5) t | = (X – 5) t |
| 3 |
⇒ X + 5 = 3X – 15
⇒ 2X = 20
⇒ X = 10 km/h
Downstream speed = 10 + 5 = 15 km/h
Upstream speed = 10 – 5 = 5 km/h
Hence, option A is correct.
Percentage
It’s used to find the amount of something in terms of 100. It’s a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign; it has no unit of measurement. It is a dimensionless number. A relative value creating hundredth parts of any quantity. One percent (symbolised) is a hundredth part, thus 100 percent represents the entirety and 200 percent specifies twice the given quantity.
Percentage Questions for NRA CET 10th (Matriculate) Level:
Ex.
The population of goa is 233280 at present. Find the population two years ago if it decreased by 10% during the first year and then it increased at the rate of 20% during the second year to reach the present population.
Percentage Questions for NRA CET 10th (Matriculate) Level:
Ex.
The population of goa is 233280 at present. Find the population two years ago if it decreased by 10% during the first year and then it increased at the rate of 20% during the second year to reach the present population.
228200
212000
216000
305600
Solution :
Let the population two years ago = x
According to question,
Solution :
Let the population two years ago = x
According to question,
| x × | 90 | × | 120 | = 233280 |
| 100 | 100 |
| x = | 233280 × 100 × 100 | = 216000 |
| 90 × 120 |
Hence, option (C) is correct.
Percentage Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
In an examination Tarang got 25% marks and failed by 64 marks. If he had got 40% marks he would have secured 32 marks more than the pass marks. Find the percentage of pass marks.
Ex.
In an examination Tarang got 25% marks and failed by 64 marks. If he had got 40% marks he would have secured 32 marks more than the pass marks. Find the percentage of pass marks.
224 marks
250 marks
150 marks
295 marks
Solution :
Solution :
Let the total marks = x
According to the question,
x × 25% + 64 = x × 40% – 32
x × 40% - x × 25% = 64 + 32
x × 15% = 96
x = 640
Passing marks = 640 × 25% + 64
= 160 + 64 = 224 marks
Hence, option A is correct.
Percentage Questions for NRA CET Graduate Level :
Ex.
In a school number of students in 6th and 7th class is in the ratio 6 : 11. If 60% of total students in class 6 are boys and 52% of total students in class 7 are boys, then find total girls in both the class together is approximately what percentage of total students in both the classes?
39.4
45.2
49.9
35.6
Solution :
Let total students in class 6th and class 7th is 6x and 11x respectively.
Total students in both classes = 6x + 11x = 17x
Let total students in class 6th and class 7th is 6x and 11x respectively.
Total students in both classes = 6x + 11x = 17x
| Girls in class 6 = 6x × | 40 | = | 240x | = 2.4x |
| 100 | 100 |
| Girls in class 7 = 11x × | 48 | = | 528x | = 5.28x |
| 100 | 100 |
So total girls = 2.4x + 5.28x = 7.68x
| Reqd. % = | 7.68x | × 100 ⇒ 45.2% (approx.) |
| 17x |
Hence, option B is correct.
Mixture and Allegation
Allegation – It refers to a rule that helps to find the ratio in which two or more at a given price are mixed to produce a mixture of specified price.
Means Price - It has the cost price of a unit quantity of a mixture which is prepared by mixing two or more ingredients.
Allegation Rule –It says that if two ingredients at a given price are mixed to produce a mixture at the given price, the ratio of quantity of cheaper ingredient and quantity of dearer ingredients.
It enables us to find the ration in which two or more ingredients at the given price must be mixed to produce a mixture of desired place.
Means Price - It has the cost price of a unit quantity of a mixture which is prepared by mixing two or more ingredients.
Allegation Rule –It says that if two ingredients at a given price are mixed to produce a mixture at the given price, the ratio of quantity of cheaper ingredient and quantity of dearer ingredients.
It enables us to find the ration in which two or more ingredients at the given price must be mixed to produce a mixture of desired place.
Mixture and Allegation Questions for NRA CET 10th (Matriculate) Level:
Ex.
A bucket contained a mixture of two liquids P and Q in the ratio of 4 : 1. When 10 litres of the mixture is taken out and 10 litres of the liquid Q was added to the bucket, Ratio becomes 2 : 3. Find the initial quantity of Q.
Ex.
A bucket contained a mixture of two liquids P and Q in the ratio of 4 : 1. When 10 litres of the mixture is taken out and 10 litres of the liquid Q was added to the bucket, Ratio becomes 2 : 3. Find the initial quantity of Q.
6 litres
5 litres
4 litres
7 litres
Solution :
Let initial quantites of P and Q be 4x & x.
| P | = | 4x |
| Q | x |
In 10 litres of mixture, quantity of liquid P = 4/5 x 10 = 8, therefore quantity of liquid Q = 2
When 10 litres of mixture taken out & 10 litres liquid Q is added, we get
| P | = | 4x – 8 | = | 2 |
| Q | x – 2 + 10 | 3 |
⇒ 12x – 24 = 2x + 16
⇒ 10x = 24 + 16
| x = | 40 | = 4 litres |
| 10 |
So, the initial quantity of liquid Q was = 1x = 4 litres
Hence, option C is correct
Mixture and Allegation Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
A solution of ‘THANDA SHARBAT’ has 15% sugar. Another solution has 5% sugar. How many liters’ of the second solution must be added to the 20L of first solution to make a solution of 10 % sugar?
Ex.
A solution of ‘THANDA SHARBAT’ has 15% sugar. Another solution has 5% sugar. How many liters’ of the second solution must be added to the 20L of first solution to make a solution of 10 % sugar?
10 L
5 L
15 L
20 L
Solution :
Let required amount of second solution to be added = a L
Solution :
Let required amount of second solution to be added = a L
| Then | 15 × 20 + 5a | = 10 |
| 20 + a |
⇒ 300 + 5a = 200 + 10a
⇒ 5a = 100
⇒ a = 20
Hence, option (D) is correct.
Mixture and Allegation Questions for NRA CET Graduate Level :
Ex.
A milkman completely fills his 24 liter cistern with two type of milks A and B in the ratio 7 : 5. The cost price of type A milk is Rs.45 per liter. If he sold this mixture at the rate of Rs.56 per liter at a profit of 12%, then find the per liter cost price of type B milk.
Rs. 54
Rs. 47
Rs. 62
Rs. 57
Solution :
| Quantity of type A milk = 24 × | 7 | = 14 liters |
| 12 |
| Quantity of type B milk = 24 × | 5 | = 10 liters |
| 12 |
SP of mixture = 24 × 56 = Rs.1344
CP of mixture when sold at 12% profit
| = 1344 × | 100 | = Rs.1200 |
| 112 |
CP of type A milk = 14 × 45 = Rs.630
CP of type B milk = Rs. (1200 – 630) = Rs.570
| Per liter CP of type B milk = | 570 | = Rs. 57 |
| 10 |
Hence, option D is correct.
Inequalities
When there are certain coded relationships denoted by specific symbols. It simply means a mathematical expression in which the sides are not equal to each other. Basically an inequality compares any two values and show the one values is less than, greater than or equal to the value on the other side of the equation.
Inequalities Questions for NRA CET 12th (Higher Secondary) Level :
Ex.
Ex.
Quantity I : What was his average speed (in meters per second) for the entire journey?
Quantity II : 12.5
Quantity: I > Quantity: II
Quantity: I ≥ Quantity: II
Quantity: I < Quantity: II
Quantity: I ≤ Quantity: II
Solution :
Let the total distance = 3x km
The time taken to cover one–third i.e. x km
Solution :
Let the total distance = 3x km
The time taken to cover one–third i.e. x km
| = | x | hour |
| 24 |
The time taken to cover the remaining distance 2x km=
| = | 2x | hours |
| 48 |
| The average speed = | Total distance |
|
Total time
|
| = | 3x |
| x/24 + x/24 |
| = 3x × | 12 | = 36 km/hour |
| x |
Quantity I: the average speed in meter per sec
| = 36 × | 5 | = 10 meters/second |
| 18 |
Quantity II: 12.5 meter per sec
Therefore, Q1 < Q2
Hence, option C is correct.
Inequalities Questions for NRA CET Graduate Level :
Ex.
Ex.
Quantity I : The length of the diagonal of a rectangle is three – fifth of the side of a square of area 756.25 sq. cm. If the length of the rectangle is 3.3 cm more than that of the breadth, then what is the area of the rectangle?
Quantity II : 125 sq. cm
Quantity : I > Quantity : II
Quantity : I ≥ Quantity : II
Quantity : I < Quantity : II
Quantity : II ≥ Quantity : I
Solution :
Quantity : I
The sides of the square = 756.25 = 27.5 cm
Solution :
Quantity : I
The sides of the square = 756.25 = 27.5 cm
| The diagonal of the rectangle = | 3 × 27.5 | = 16.5 cm |
| 5 |
Let length = l cm then breadth = (l – 3.3) cm
We know that, in a rectangle, diagonal2 = l2 + b2
16.5 = (l2 + (l – 3.3)2
272.25 = l2 + (l – 3.3)2
By solving, l = 13.2 cm
b = (13.2 – 3.3) = 9.9 cm
Area = l × b = 13.2 × 9.9 = 130.68 sq. cm
Quantity II : 125 sq. cm
Therefore, Quantity : I > Quantity : II
Hence, option A is correct.
Number Series
An ordered list of numbers governed by a pattern or rule. It presents with mathematical sequence that follow a logical rule based on elementary arithmetic.
In these questions a sequence meet a specific logical rule which needs to be recognized in order to find the missing terms..
Levels of complexity
The difficult level of numbers sequence questions may increase in several ways
1. The rule behind the sequence becomes less significant.
2. Log Sequence usually the longer the sequence the more complex the question is
3. The missing term appears early in sequence rather than a later.
In these questions a sequence meet a specific logical rule which needs to be recognized in order to find the missing terms..
Levels of complexity
The difficult level of numbers sequence questions may increase in several ways
1. The rule behind the sequence becomes less significant.
2. Log Sequence usually the longer the sequence the more complex the question is
3. The missing term appears early in sequence rather than a later.
Number Series Questions for NRA CET 10th (Matriculate) Level:
Ex.
If the first term of a series is – 12 and the 15th term of the series is 28 then what is the 29th term of the series?
78
56
88
68
Solution :
First term = – 12, 15th term = 28
tn = nth term = a + (n – 1) d
a = first term = – 12, n = number of term = 15 d = common difference, tn = nth term = 15th term = 28
therefore, 28 = – 12 + 14d
Ex.
If the first term of a series is – 12 and the 15th term of the series is 28 then what is the 29th term of the series?
78
56
88
68
Solution :
First term = – 12, 15th term = 28
tn = nth term = a + (n – 1) d
a = first term = – 12, n = number of term = 15 d = common difference, tn = nth term = 15th term = 28
therefore, 28 = – 12 + 14d
| d = | 40 | = | 20 |
| 14 | 7 |
| 29th term = | – 12 + (29 – 1) × 20 | = – 12 + 80 = 68 |
| 7 |
Hence, option D is correct.
Number Series Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
143 151 158 172 182 ?
192
193
190
191
Solution :
Ex.
143 151 158 172 182 ?
192
193
190
191
Solution :
| Series Pattern | Given Series | |
| 143 | 143 | |
| 143 + (1 + 4 + 3) = 151 | 151 | |
| 151 + (1 + 5 + 1 ) = 158 | 158 | |
| 158 + (1 + 5 + 8) =172 | 172 | |
| 172 + (1 + 7 + 2) = 182 | 182 | |
| 182 + (1 + 8 + 2) = 193 | 193 | ? |
Hence, option (D) is correct.
Number Series Questions for NRA CET Graduate Level :
Ex.
1, 5, 19, 81, ?, 2473
814
389
675
411
Solution :
| Series Pattern | Given Series | |
| 1 | 1 | |
| 1 × 2 + 3 = 5 | 5 | |
| 5 × 3 + 4 = 19 | 19 | |
| 19 × 4 + 5 = 81 | 81 | |
| 81 × 5 + 6 = 411 | 411 | ? |
| 411 × 6 + 7 = 2473 | 2473 |
Hence, option (D) is correct.
Simple Interest
It’s the interest charged on the loan. It’s a quick and easy method of calculating the interest charge on a loan. Simple Interest is determined by multiplying the daily interest rate by the principal by the number of days that elapse between payments.
Simple Interest Questions for NRA CET 10th (Matriculate) Level:
Ex.
At what rate percentage per annum will the simple interest on a sum of money be 7/9 of the amount in 7 years?
10%
20%
40%
50%
Solution :
Ex.
At what rate percentage per annum will the simple interest on a sum of money be 7/9 of the amount in 7 years?
10%
20%
40%
50%
Solution :
| S.I. = | P × R × T |
| 100 |
| As, Amount = P + | PRT |
| 100 |
So, According to given condition :-
| ⇒ S.I. = | 7 | (Amount) |
| 9 |
| PRT | = | 7 | ( | P + | PRT | ) |
| 100 | 9 | 100 |
| PRT | = | 7P | ( | 1 + | RT | ) |
| 100 | 9 | 100 |
| R | = | 1 | + | RT |
| 100 | 9 | 900 |
| R | – | 7R | = | 1 | ⇒ | 900R – 700R | = | 1 |
| 100 | 900 | 9 | 90000 | 9 |
⇒ 200 R = 10,000
R = 50%
Hence, option (D) is correct.
Simple Interest Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
The simple interest received on a sum of money at the end of 10 years is two times of the principal. At the same rate of interest, what would be the ratio of principal and compound interest received at the end of two years?
Ex.
The simple interest received on a sum of money at the end of 10 years is two times of the principal. At the same rate of interest, what would be the ratio of principal and compound interest received at the end of two years?
20 : 11
20 : 9
25 : 11
25 : 9
Solution:
Let the principal = Rs. 100x
Then, according to the question, SI = 2 × 100x = 200x
| SI = | P × R × T |
| 100 |
| 200x = | 100x × R × 10 |
| 100 |
R = 20%
The CI on Rs. 100x for 2 years
| = 100x | ( | 1 + | 20 | ) | 2 | – 100x = 44x |
| 100 |
The required ratio = 100x : 44x = 25 : 11
Hence, option C is correct.
Simple Interest Questions for NRA CET Graduate Level :
Ex.
From a bank, Ram and Shyam together took a certain amount under simple interest and they lent the total amount to Mohan at 2% more simple interest. At the end of 4 years, the total money earned by Ram after paying the interest to the bank was Rs. 400 more than that of Shyam. From the bank, the total amount taken by Ram was how much more than that of Shyam?
Rs. 10000
Rs. 20000
Rs. 5000
Rs. 25000
Solution :
Let Ram took Rs. a and Shyam took Rs. b
Let the rate of interest was r% per annum
They lent Rs. (a + b) to Mohan at the rate of (r + 2)% per annum
For Ram,
| The total interest received on Rs. a = a × 4 × | r + 2 |
| 100 |
| The total interest paid by Ram to the bank = a × r × | 4 |
| 100 |
The total interest earned by Ram after paying the interest to the bank
| = a × 4 × | r + 2 | – a × r × | 4 | = | 8a | ------ (i) |
| 100 | 100 | 100 |
For Shyam,
| The total interest received on Rs. b = b × 4 × | r+ 2 |
| 100 |
| The total interest paid by Shyam to the bank = b × r × | 4 |
| 100 |
The total interest earned by Ram after paying the interest to the bank
| = b × 4 × | r + 2 | – b × r × | 4 | = | 8b | ------ (ii) |
| 100 | 100 | 100 |
From the question,
| 8a | – | 8b | = 400 |
| 100 | 100 |
a – b = 50 × 100 = Rs. 5000
Hence, option C is correct.
Profit and Loss
It displays the net profit and loss of a business over a specified period of time. The profit and loss statement is a financial statement that summarizes the revenues, costs and expenses incurred during a specific period, usually a fiscal quarter or year.
Profit and loss Questions for NRA CET 10th (Matriculate) Level:
Ex.
An item of cost price Rs 23000 is marked at Rs 29000. After allowing a discount of d% a profit of 16% is made. What is the value of d?
12%
8%
10%
16%
Solution :
Selling price for a profit of 16%
Ex.
An item of cost price Rs 23000 is marked at Rs 29000. After allowing a discount of d% a profit of 16% is made. What is the value of d?
12%
8%
10%
16%
Solution :
Selling price for a profit of 16%
| = 23000 × | 116 | = Rs 26680 |
| 100 |
Therefore discount = 29000 – 26680 = Rs 2320
Discount percent = d
| Then, 29000 × | d | = 2320 |
| 100 |
d = 8%
Hence, option (B) is correct.
Profit and loss Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
A shopkeeper purchased 50 dozen bottles for Rs.3000. Out of these, 60 bottles were broken and could not be sold. At what rate per dozen should he sell the remaining bottles to make a profit of 20%?
Ex.
A shopkeeper purchased 50 dozen bottles for Rs.3000. Out of these, 60 bottles were broken and could not be sold. At what rate per dozen should he sell the remaining bottles to make a profit of 20%?
Rs. 60
Rs. 75
Rs. 80
Rs. 90
Solution :
Since there are 12 quantities in a dozen
Solution :
Since there are 12 quantities in a dozen
| ⇒ dozen of bottles broken = | 60 | = 5 dozen |
| 12 |
| Required amount to gain 20% profit = Rs 3000 × | 120 | = Rs 3600 |
| 100 |
Since shopkeeper has to gain this amount by selling remaining 45 dozen of bottles
| ⇒ S.P. Per Dozen = Rs | 3600 | = Rs. 80 |
| 45 |
Hence, option (C) is correct.
Profit and loss Questions for NRA CET Graduate Level :
Ex.
A dealer incurred a loss of 20%, when he allowed a discount of 25% on marked price of an article. Then what per cent discount should he allow on the marked price so as to gain Rs. 900 on the article, if the marked price of the article is Rs. 40,000?
4%
7%
6%
3%
Solution :
SP when 25% discount is allowed = 75% of 40,000 = Rs. 30,000
CP when there is loss of 20%
A dealer incurred a loss of 20%, when he allowed a discount of 25% on marked price of an article. Then what per cent discount should he allow on the marked price so as to gain Rs. 900 on the article, if the marked price of the article is Rs. 40,000?
4%
7%
6%
3%
Solution :
SP when 25% discount is allowed = 75% of 40,000 = Rs. 30,000
CP when there is loss of 20%
| = 30000 × | 100 | = Rs. 37500 |
| 80 |
SP to gain Rs.900 = Rs. (37500 + 900) = Rs. 38400
New Discount = Rs. (40000 – 38400) = Rs. 1600
| Discount % = 1600 × | 100 | = 4% |
| 40000 |
Hence, option E is correct.
Problems of Ages
They are very frequent in competitive exams, it may seems to be complicated but with practice it becomes easy.
Problems on Ages Questions for NRA CET 10th (Matriculate) Level:
Ex.
Ex.
The average age of 5 sons in a family is 9 years. Average age of sons and parents is 24 years. If father is 9 years older than the mother, then find the age of the father after 17 years.
74 years
83 years
78 years
66 years
Solution :
The average age of 5 sons in a family is 9 years.
Total age of 5 sons = 45 years
Average age of sons and parents is 24 years.
Total age of 5 sons, father's and mother's = 24 × 7 = 168 years
Total age of father and mother = 168 – 45 = 123 years
Let the mother's age = x, then father's age = x + 9
x + x + 9 = 123
2x = 114
x = 57 years
Hence father's age after 17 years = 57 + 9 + 17 = 83 years
Therefore, option (B) is correct.
Problems on Ages Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Ex.
At present, five times of the age of Rahul is equal to three times of the age of Rocky. The age of Rocky’s wife is 5 years less than that of Rocky. 5 years ago, the ratio of the age of Rahul and Rocky’s wife was 2 : 3. At present, what is the average age of Rahul, Rocky and his wife?
25 years
30 years
20 years
15 years
Solution :
At present, five times of the age of Rahul is equal to three times of the age of Rocky
Rahul’s age: Rocky’s age = 3 : 5
Let the age of Rahul = 3x years then the age of Rocky = 5x years
The age of Rocky’s wife = 5x – 5 years,
5 years ago, the age of Rahul = 3x – 5 years
The age of Rocky’s wife = 5x – 5 – 5 years
| 3x – 5 | = | 2 |
| 5x – 10 | 3 |
9x – 15 = 10x – 20
x = 5 years
At present, the sum of their age = 3x + 5x + 5x – 5 years = 13x – 5 = 65 – 5 = 60 years
| The reqd. average = | 60 | = 20 years |
| 3 |
Hence, option C is correct.
Problems on Ages Questions for NRA CET Graduate Level :
Ex.
Ex.
There are three members in a family – husband, wife and their son. Husband’s age is thrice his son’s age and wife is three years younger than his husband. What is the respective ratio of ages of son, husband and wife if their average age is 41?
17 : 9 : 18
15 : 4 : 12
6 : 18 : 17
4 : 12 : 15
Solution :
Solution :
Let son’s age = x
Husband’s age = 3x
Wife’s age = 3x – 3
According to question-
⇒ x + 3x + (3x – 3) = 41 × 3
⇒ 7x = 126
⇒ X = 18
Son’s age = 18 years
Husband’s age = 18 × 3 = 54 years
Wife’s age = 18 × 3 – 3 = 51 years
Required ratio = 18 : 54 : 51 = 6 : 18 : 17
Hence, option C is correct.
Probability
How likely a proposition is true or events. It is a part of mathematics which deals with the occurrence of a random event. The probability of an event is a number between 0 and 1, where roughly speaking, 0 indicates impossibilities of the event and 1 indicates certainty. The higher the probability of an event the more likely it is that the event will occur. Simple example is the tossing of a fair unbiased coin. Since the coin is fair, the two outcomes are both equally probable. The probability of heads equals the probability of tails and since no other outcomes are possible, the probability of either heads or tails is ½.
Probability Questions for NRA CET 10th (Matriculate) Level:
Ex.
Ex.
A bag contains 24 red and 10 black balls. Two balls are drawn at random. What is the probability that they are of the same color?
141/168
27/168
129/144
107/187
Solution :
Total number of balls = 24 + 10 = 34
Number of ways to pick 2 balls from 34 balls = 34C2 = 561
Number of red balls = 24
Number of ways to pick 2 balls from 24 balls = 24C2 = 276
Number of black balls = 10
Number of ways to pick 2 balls from 10 balls = 10C2 = 45
∴ the probability that both are same color
| = | 276 + 45 | = | 107 |
| 561 | 187 |
Hence, option D is correct.
Probability Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Three dice are thrown together. Find the probability of getting a total of at least 6 ?
Ex.
Three dice are thrown together. Find the probability of getting a total of at least 6 ?
103/216
103/208
103/108
36/103
Solution :
Since one die can be thrown in six ways to obtain any one of the six numbers marked on its six faces
⇒ Total number of elementary events = 6 x 6 x 6 = 216
Let A be the event of getting a total of at least 6.Then A denotes the event of getting a total of less than 6 i.e. 3, 4, 5.
⇒ A = { (1,1,1), (1,1,2), (1,2,1), (2,1,1), (1,1,3),(1,3,1), (3,1,1), (1,2,2), (2,1,2), (2,2,1) }
So, favorable number of cases = 10
Solution :
Since one die can be thrown in six ways to obtain any one of the six numbers marked on its six faces
⇒ Total number of elementary events = 6 x 6 x 6 = 216
Let A be the event of getting a total of at least 6.Then A denotes the event of getting a total of less than 6 i.e. 3, 4, 5.
⇒ A = { (1,1,1), (1,1,2), (1,2,1), (2,1,1), (1,1,3),(1,3,1), (3,1,1), (1,2,2), (2,1,2), (2,2,1) }
So, favorable number of cases = 10
| ⇒ P(A) = | 10 |
| 216 |
| ⇒ 1 – P (A) = | 10 |
| 216 |
| ⇒ P(A) = 1 – | 10 |
| 216 |
| = | 103 |
| 108 |
Hence, option (C) is correct.
Probability Questions for NRA CET Graduate Level :
Ex.
Ex.
In how many ways can the walls of a cuboidal box be painted using six different colours using one colour for each wall if six different symbols are carved on the box with one on each wall?
240
560
720
360
Solution :
No. of ways in which the walls of the box can be painted using six different colours = 6! = 720
No. of ways in which the walls of the box can be painted using six different colours = 6! = 720
Hence, option C is correct.
Permutation and Combination
Permutation is the act of arranging all the member of a set into some sequence or order.
Combination is a way of selecting items from a collection, the order of selection does not matter.
Both of them together defines the various ways to arrange a certain group of data. This selection of subsets is called a permutation when the order of selection is a factor; a combination when order is not a factor. By considering the ratio of the number of desired subsets to the number of all the possible subsets for many games of chance.
Combination is a way of selecting items from a collection, the order of selection does not matter.
Both of them together defines the various ways to arrange a certain group of data. This selection of subsets is called a permutation when the order of selection is a factor; a combination when order is not a factor. By considering the ratio of the number of desired subsets to the number of all the possible subsets for many games of chance.
Permutation and Combination Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
How many 3 - letter words with or without meaning, can be formed out of the letters of the word, 'LOGARITHMS', if repetition of letters is not allowed?
720
420
5040
120
Solution :
The word 'LOGARITHMS'' has 10 different alphabets
Hence, the number of 3-letter words (with or without meaning) formed by using these letters = (10P3)
= 10 × 9 × 8 = 720
Therefore, option (A) is correct.
Permutation and Combination Questions for NRA CET Graduate Level :
Ex.
Five people out of whom only two can drive are to be seated in a five seater car with two seats in front and three in the rear. The people who know driving don’t sit together. Only someone who knows driving can sit on the driver’s seat. Find the number of ways the five people can be seated.
40
60
48
36
Solution :
Number of people who can drive = 2
Number of ways of selecting driver = 2C1
The other person who knows driving can be seated only in the rear three seats in 3 ways
Total number of ways of seating the two persons = 2C1 × 3
Number of ways of seating remaining = 3!
Total number of all five can be seated = 2C1 × 3 × 3! = 36
Hence, correct answer is 36
Hence, option D is correct.
Problems of Trains
It’s an integral part of the time and speed questions. They require a different approach and are not same as the basic speed and distance question. Similar to the concept of speed, distance time, train problems are specifically based on evaluating the speed, distance covered and time is taken by a train under different conditions. The weightage of questions asked from this topic in the quantitative aptitude sections of various government exams is mostly between 1-3 marks and the common exams which includes this topic.
Problems on Trains Questions for NRA CET 10th (Matriculate) Level:
Ex.
Two trains of same length are running on parallel tracks in opposite directions with speed 48 km/hr and 72 km/hr respectively. They cross each other in 12 seconds. The length of each train is –
200m
115m
225m
150m
Solution :
Two trains of same length are running on parallel tracks in opposite directions with speed 48 km/hr and 72 km/hr respectively.
Let the length of each train be x metre.
We know,
| Distance = Speed × Time → Time = | Distance |
| Speed |
If two trains are going towards each other, then their relative speed = Summation of their speeds
So, relative speed = (48 + 72) km/h = 120 km/hr
| = 120 × | 1000 | = | 100 | metre/second |
| 3600 | 3 |
Now we can write,
| 2x | = 12 |
| 100/3 |
| ⇒ 2x = 12 × | 100 |
| 3 |
⇒ 2x = 400
⇒ x = 200
∴ The length of each train = 200 metre.
Hence, option (A) is correct.
Hence, option (A) is correct.
Problems on Trains Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Ex.
A train Pawan express of length 380 m running with the speed of 108 km/h crosses a platform of certain length in 37 seconds. Another train, Toofan express of certain length running with a speed of 90 km/h crosses the platform in 42.6 seconds. What will be the time taken by both trains to cross each other if they run in opposite directions.
12 seconds
10 seconds
13 seconds
9 seconds
Solution :
| Speed of Pawan express = | 5 | × 108 = | 30m |
| 18 | s |
Let, length of the platform = x m
And, length of the Toofan express = y m
| So, | 380 + x | = 37 |
| 30 |
So, 380 + x = 1110
x = 1110 – 380 = 730
| Speed of Toofan Express = | 5 | × 90 = 25 | m |
| 18 | s |
| So, | y + 730 | = 42.6 |
| 25 |
= y + 730 = 1065
= y =1065 – 730 = 335 m
| Therefore, reqd. time = | 380 + 335 | = | 715 | = 13 seconds |
| 30 + 25 | 55 |
Hence, option C is correct.
Problems on Trains Questions for NRA CET Graduate Level :
Ex.
Ajay walked 12 km to reach the station from his house. Then he boarded in a train and reached his destination. The average speed of the entire journey was 62 kmph and he took a total time of 6 hours. If the average speed of train was 120 kmph, then what is the ratio of walking speed of Ajay to the speed of train?
1 : 30
1 : 60
2 : 35
2 : 65
Solution :
Let the time travelled in train be 'x' hours
Total distance = 62 × 6 = 12 + 120 × x
⇒ 372 = 12 + 120x
⇒ x = 3
So, Ajay walked for (6-3) = 3 hours
Walking speed of Ajay
Solution :
Let the time travelled in train be 'x' hours
Total distance = 62 × 6 = 12 + 120 × x
⇒ 372 = 12 + 120x
⇒ x = 3
So, Ajay walked for (6-3) = 3 hours
Walking speed of Ajay
| = | Distance covered by walking | = | 12 | = 4 kmph |
| Time taken by walking | 3 |
Required ratio = 4 : 120 = 1 : 30
Hence, option A is correct.
Data Sufficiency
The first part is to understand the meaning of the options and commit them to memory. It tests your basic knowledge of maths facts. It involves very simple calculations; This does not mean that the questions are very simple.
A data sufficiency question set will contain the following:
A data sufficiency question set will contain the following:
- Instructions
- Questions
- Two statements
Data Sufficiency Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Directions: Each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read all the statements and give answer:
Ex.
Directions: Each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read all the statements and give answer:
What is the time shown by the clock right now?
Statement I : The hour hand is in between 3:00 and 4:00 O’clock and the angle between the two hands is 100°..
Statement II : The hour hand is between 5:00 and 6:00 O’clock and the angle between the two hands is 160°.
If the data in statement I alone is sufficient to answer the question, while the data in statement II alone is not sufficient to answer the question
If the data in statement II alone is sufficient to answer the question, while the data in statement I alone is not sufficient to answer the question
If the data either in statement I alone or in statement II alone is sufficient to answer the question
If the data in both statements I and II together are necessary to answer the question
If the data given in both statements I and II together are not sufficient to answer the question.
Solution :
If the data in statement I alone is sufficient to answer the question, while the data in statement II alone is not sufficient to answer the question
If the data in statement II alone is sufficient to answer the question, while the data in statement I alone is not sufficient to answer the question
If the data either in statement I alone or in statement II alone is sufficient to answer the question
If the data in both statements I and II together are necessary to answer the question
If the data given in both statements I and II together are not sufficient to answer the question.
Solution :
From statement I, when the time is 3:00, the angle of the hands is 90°, between 3 : 00 and 4 : 00, the angle between the hands goes on decreasing from 90 to 0, then from 0°, it increases to 180°, and then it decreases from 180°, and then it decreases from 180° to 1200 at 4:00 pm. So all the angles from 0° – 90° and 120°– 180°occur twice between 3:00 and 4:00 but angles 90°to 120° occur only once between 3:00 to 4:00 and hence time can be determined uniquely if the angle is 1000 (since 90° < 100° < 120°) same is the case with statement II also.
From, either of the statements we can answer the question.
Hence, option C is correct.
Data Sufficiency Questions for NRA CET Graduate Level:
Data Sufficiency Questions for NRA CET Graduate Level:
Ex.
Directions: Each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read all the statements and give answer:
Directions: Each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read all the statements and give answer:
What is the ratio of the total number of females to the total number of males in a Multi-National company?
Statement I : There are 45000 employees in the company out of which 45% are males.
Statement II : The ratio of the total number of females to the total number of males in the last year was 2 : 3.
The data in statements I alone is sufficient to answer the question, while the data in statement II alone is not sufficient to answer the question.
The data in statements II alone is sufficient to answer the question, while the data in statement I alone is not sufficient to answer the question.
Either Statement I or Statement II alone is sufficient to answer the question.
The data in both the statements I and II is not sufficient to answer the question.
The data in both the statements I and II together is necessary to answer the question.
Solution :
Solution :
Clearly, last year’s ratio is irrelevant if we want to find this year’s ratio.
∴ Statement II doesn’t give any relevant information to compute the answer.
Considering statement I;
Total no. of employees = 45000
Number of males = 45% of 45000 = 0.45 × 45000 = 20250
⇒ Number of females = 45000 – 20250 = 24750
∴ Ratio = 24750 : 20250 = 11 : 9
∴ Statement I is alone sufficient to answer the question.
Hence, option A is correct.
Approximation
Approximation can be applied to various properties (value, quantity, image, description) that are nearly but not exactly correct: similar, but not exactly the same. Although mostly it is applied to numbers, it is also frequently applied to mathematical functions. It occurs when a exact form or an exact numerical number is unknown or difficult to obtain. Calculations are likely to involve rounding errors leading to approximation. Log tables, slide rules, and calculators produce approximate answers to all but the simplest calculations.
Approximation Question for NRA CET 12th (Higher Secondary) Level:
Ex.
350 ÷ 14.94 × 15.86 + ? = 24.712
241
273
257
235
Solution :
Ex.
350 ÷ 14.94 × 15.86 + ? = 24.712
241
273
257
235
Solution :
350 ÷ 14.94 × 15.86 + ? = 24.712
≈ 350 ÷ 15 × 16 + ? = 252
≈ 23 × 16 + ? = 625
≈ 368 + ? = 625
≈ ? = 625 – 368 = 257
? = 257
Hence, option C is correct.
Approximation Question for NRA CET Graduate Level:
Ex.
(√7920 × √3482) – (68.06)2 = (?)2 – 48.92
Ex.
(√7920 × √3482) – (68.06)2 = (?)2 – 48.92
56
36
26
16
34
Solution :
(√7920 × √3482) – (68.06)2 = (?)2 – 48.92
(√7921 × √3481) – (68)2 ≈ (?)2 – 49
(89 × 59) – 4624 = (?)2 – 49
5251 – 4624 = (?)2 – 49
(?)2 = 627 + 49
(?)2 = 676
? = √676
? = 26
Hence, option C is correct.
Time and Work
It deals with the simultaneous performance involving the efficiency of an individual or group and the time taken by them to complete a piece of work. Work is the effort applied to produce a deliverable or accomplish a task.
A certain amount of time (T) is taken to complete a certain work (W). The number of units of work done per unit time is called the rate of work. Whenever some work is done, the total work itself can be taken as one unit.
A certain amount of time (T) is taken to complete a certain work (W). The number of units of work done per unit time is called the rate of work. Whenever some work is done, the total work itself can be taken as one unit.
Time and Work Questions for NRA CET 10th (Matriculate) Level:
Ex.
Ex.
A can do a piece of work in 4 hours. B and C can do it in 3 hours. A and C can do it in 2 hours. How long will B alone take to do it?
10 hours
12 hours
8 hours
24 hours
Solution :
| A's one hour's work = | 1 |
| 4 |
| (B + C) 's one hour's work = | 1 |
| 3 |
| (A + C) 's one hour's work = | 1 |
| 2 |
(A + B + C) 's one hour's work = 1/4 + 1/3 = 7/12
| and B's one hour's work = | 7 | – | 1 | = | 7 – 6 | = | 1 |
| 12 | 2 | 12 | 12 |
Hence, B alone con do the work in 12 hours.
Hence, option B is correct.
Time and Work Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
A can complete a piece of work in 12 days, A, B and C can complete the work in 6 days. Efficiency of B is 0.5 times the efficiency of A. In how many days C can complete the work alone?
A can complete a piece of work in 12 days, A, B and C can complete the work in 6 days. Efficiency of B is 0.5 times the efficiency of A. In how many days C can complete the work alone?
10 days
16 days
24 days
12 days
None of these
Solution :
Time taken by B to complete the work
Solution :
Time taken by B to complete the work
| = | 12 | = 24 days |
| 0.5 |
| 1 | + | 1 | + | 1 | = | 1 |
| A | B | C | 6 |
| 1 | = | 1 |
| A | 12 |
| 1 | = | 1 |
| B | 24 |
| 1 | + | 1 | + | 1 | – | 1 | – | 1 | = | 1 | – | 1 | – | 1 |
| A | B | C | A | B | 6 | 12 | 24 |
| ⇒ | 1 | = | 4 – 2 – 1 |
| C | 24 |
| ⇒ | 1 | = | 1 |
| C | 24 |
Hence, C can complete the work alone in 24 days.
Hence, option (C) is correct.
Time and Work Questions for NRA CET Graduate Level:
Ex.
2 employees and 3 trainees together can finish a project in 7 days, 6 employees and 13 trainees together can finish the same project in 2 days. Find the time taken by 4 employees and 4 trainees together to finish the same work.
4 days
5 days
6 days
8 days
9 days
Solution :
Ex.
2 employees and 3 trainees together can finish a project in 7 days, 6 employees and 13 trainees together can finish the same project in 2 days. Find the time taken by 4 employees and 4 trainees together to finish the same work.
4 days
5 days
6 days
8 days
9 days
Solution :
Let time taken by 4 employees and 4 trainees together is ‘x’.
Let one day work of one employee and one trainee is ‘E’ and ‘T’ respectively.
Total work = 7 × (2E + 3T) = 2 × (6E + 13T)
⇒ 14E + 21T = 12E + 26T
⇒ 2E = 5T …….. (1)
Total work done by 4 employees and 4 trainees together in ‘x’ days = x × (4E + 4T) = 2 × (6E + 13T)
From equation (1)-
⇒ x × (10T + 4T) = 2 × (15T + 13T)
| ⇒ x = | 56T | = 4 days |
| 14T |
Hence, option A is correct.
Average
Is a list of data is the expression of the central value of a set of data. Mathematically, it is defined as the ratio of summation of all the data to the numbers of units present in the list.
An average of a list of data is the expression of the central value of a set of data. It is defined as the ratio of summation of all the data to the number of units present in the list.
An average of a list of data is the expression of the central value of a set of data. It is defined as the ratio of summation of all the data to the number of units present in the list.
Average Questions for NRA CET 10th (Matriculate) Level:
Ex.
Average of 40 numbers is 25. Average of first 25 numbers is 30. Average of next 13 numbers is 15. Find the sum of the last two numbers?
50
55
58
60
Solution :
Ex.
Average of 40 numbers is 25. Average of first 25 numbers is 30. Average of next 13 numbers is 15. Find the sum of the last two numbers?
50
55
58
60
Solution :
Average of 40 numbers = 25
So, sum of all 40 numbers = 40 × 25 = 1000
Average of first 25 number is 30
So, sum of first 25 number = 25 × 30 = 750
Average of Next 13 number = 15
Sum = 13 × 15 = 195
So, sum remaining last 2 number = 1000 – 750 + 195 = 55
Hence, option (B) is correct.
Average Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Ex.
Average of a set of five consecutive even numbers is 48. Average of another set of five consecutive odd numbers is 49. Find the product of smallest even number of the first set and largest odd number of the second set.
3223
2323
3232
2332
None of these
3223
2323
3232
2332
None of these
Solution :
Average of n consecutive even/odd numbers
⇒ a = first number + (n – 1)
⇒ 48 = first number + (5 – 1)
⇒ first number = 44
Even numbers are: 44, 46, 48, 50, 52
And
a = first number + (n – 1)
⇒ 49 = first number + (5 – 1)
⇒ first number = 45
Odd numbers are: 45, 47, 49, 51, 53
Required product = 44 × 53 = 2332
Hence, option (D) is correct.
Average Questions for NRA CET Graduate Level:
Ex.
In an office some persons are officers and some are non-officer. The number of officers is 30. The average salary of officers is Rs.1040 and that of non-officers is Rs.400. If the average salary of entire staff in office (officers + Non – officers) is Rs.500 per month, then what is the average of total number of employees (officers + Non – officers) in the office?
In an office some persons are officers and some are non-officer. The number of officers is 30. The average salary of officers is Rs.1040 and that of non-officers is Rs.400. If the average salary of entire staff in office (officers + Non – officers) is Rs.500 per month, then what is the average of total number of employees (officers + Non – officers) in the office?
49
89
92
96
None of these
Solution :
Let the number of non-officers in office = x
Now, according to question-
⇒ 400x + 1040 × 30 = 500(30 + x)
⇒ 400x + 1040 × 30 = 500 × 30 + 500x
⇒ 100x = 30 (1040 – 500)
⇒ 100x = 30(540)
⇒ x = 162
| Reqd. average = | 30 + 162 | = 96 |
| 2 |
Hence, option D is correct.
Quadratic Equation
It’s a type of problem that deals with a variable multiplied by itself –an operation known as squaring. This language derives from the area of a square being its side length multiplied by itself. The word quadratic comes from quadratum.
Quadratic Equations characterize a great number of phenomenon is the real world, such as where a rocket ship will land, how much to charge for a product or how long it will take a person to row up and down a river.
Quadratic Equations characterize a great number of phenomenon is the real world, such as where a rocket ship will land, how much to charge for a product or how long it will take a person to row up and down a river.
Quadratic Equation Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
Directions: In each of these questions, two equations (I) and (II) are given. You have to solve both the equations and give answer.
I. x2 – 5x + 6 = 0
II. 4y2 – 13y + 9 = 0
if x > y
if x ≤ y
if x ≥ y
if x < y
if x = y or relationship between x and y can't be established
Solution :
Solution :
I. x2 – 5x + 6 = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2, 3
II. 4y2 – 13y + 9 = 0
⇒ (4y – 9) (y – 1) = 0
| ⇒ y = | 9 | , 1 |
| 4 |
While comparing the root values of x and y, we find that one root value of x lies between y's. Therefore, relationship between x and y cannot be determined.
Hence, option (E) is correct.
Quadratic Equation Questions for NRA CET Graduate Level:
Quadratic Equation Questions for NRA CET Graduate Level:
Ex.
Directions: In each of these questions, two equations (I) and (II) are given. You have to solve both the equations and give answer.
Directions: In each of these questions, two equations (I) and (II) are given. You have to solve both the equations and give answer.
I. 10x2 – 69x + 108 = 0
II. 6y2 – 47y + 77 = 0
if x > y
if x ≤ y
if x ≥ y
if x < y
if x = y or relationship between x and y can't be established
Solution :
Solution :
I. 10x2 – 69x + 108 = 0
⇒ 10x2 – 45x – 24x + 108 = 0
⇒ 5x (2x – 9) – 12 (2x – 9) = 0
⇒ (5x – 12) (2x – 9) = 0
⇒ (5x – 12) (2x – 9) = 0
| ∴ x = | 12 | , | 9 |
| 5 | 2 |
II. 6y2 – 47y + 77 = 0
⇒ 6y2 – 33y – 14y + 77 = 0
⇒ 3y (2y – 11) – 7 (2y – 11) = 0
⇒ (3y – 7) (2y – 11) = 0
⇒ (3y – 7) (2y – 11) = 0
| ∴ y = | 7 | , | 11 |
| 3 | 2 |
on comparing the values of x and y, we get
| x | y | |
| 12 | > | 7 |
| 5 | 3 | |
| 12 | < | 11 |
| 5 | 2 | |
| 9 | > | 7 |
| 2 | 3 | |
| 9 | < | 11 |
| 2 | 2 |
Hence, either x = y or relationship cannot be established.
Hence, option E is correct.
Ratio and Proportion
It is based on fractions. When a fraction is represented in the form of then it is a ratio whereas a proportion states that two ratios are equal. Here a, and bare any two integers. The ratio and proportion are the two important concepts, and it’s is the foundation to understand the various concepts in mathematics as well in science.
In certain situations, the comparison of two quantities by the method of division is very efficient. We can say that the comparison or simplified form of two quantities.
In certain situations, the comparison of two quantities by the method of division is very efficient. We can say that the comparison or simplified form of two quantities.
Ratio and Proportion Questions for NRA CET 10th (Matriculate) Level:
Ex.
Ratio of monthly incomes of A and B is 6 : 5 and their monthly expenditures are in the ratio 4 : 3. If each of them saves Rs. 500 per month. Find the sum of their monthly incomes?
2700
2750
2600
2300
Solution :
Let the monthly incomes of A and B be 6x & 5x respectively.
Let the monthly expenditures of A and B be 4y & 3y
Income – expenditure = Saving
⇒ Income of A – Expenditure of A = Saving of A ..........................(i)
⇒ Income of B – Expenditure of B = Saving of B .........................(ii)
As, saving of A = Saving of B
So, solving (i) and (ii)
we get
⇒ (6x – 4y) × 3 = 500 × 3
(5x – 3y) × 4 = 500 × 4,
18x – 12 y = 1500
– 20x + 12y = – 2000 ...Subtracting
– 2x = – 500
⇒ x = 250
Sum of monthly incomes ⇒
6x + 5x = 11x = 11 × 250 = 2750
Hence, option (B) is correct.
Ex.
Ratio of monthly incomes of A and B is 6 : 5 and their monthly expenditures are in the ratio 4 : 3. If each of them saves Rs. 500 per month. Find the sum of their monthly incomes?
2700
2750
2600
2300
Solution :
Let the monthly incomes of A and B be 6x & 5x respectively.
Let the monthly expenditures of A and B be 4y & 3y
Income – expenditure = Saving
⇒ Income of A – Expenditure of A = Saving of A ..........................(i)
⇒ Income of B – Expenditure of B = Saving of B .........................(ii)
As, saving of A = Saving of B
So, solving (i) and (ii)
we get
⇒ (6x – 4y) × 3 = 500 × 3
(5x – 3y) × 4 = 500 × 4,
18x – 12 y = 1500
– 20x + 12y = – 2000 ...Subtracting
– 2x = – 500
⇒ x = 250
Sum of monthly incomes ⇒
6x + 5x = 11x = 11 × 250 = 2750
Hence, option (B) is correct.
Ratio and Proportion Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
In a company there are 78000 employees out of which males and females are in the ratio 7 : 6. Out of the males 35% are working as HR and out of females 25% are working as HR. Find the total number of employees working as HR in the company.
25700
27700
23500
23700
None of these
Solution :
Number of males in the company
Ex.
In a company there are 78000 employees out of which males and females are in the ratio 7 : 6. Out of the males 35% are working as HR and out of females 25% are working as HR. Find the total number of employees working as HR in the company.
25700
27700
23500
23700
None of these
Solution :
Number of males in the company
| = | 7 | × 78000 = 42000 |
| 13 |
Number of males working as HR
| = | 35 | × 42000 = 14700 |
| 100 |
Number of females in the company
| = | 6 | × 78000 = 36000 |
| 13 |
Number of females working as HR
| = | 25 | × 36000 = 9000 |
| 100 |
Total number of employees working as HR = 14700 + 9000 = 23700
Hence, option (D) is correct.
Ratio and Proportion Questions for NRA CET Graduate Level:
Ex.
In the income statement of Asha and Ravenna, the ratio of their income in the year 2017 was 5 : 4. The ratio of Asha’s income in the year 2018 to that in 2017 is 3 : 5 and the ratio of Ravenna’s income in the year 2018 to that in 2017 is 3 : 2. If Rs. 10242 is the sum of the income of Asha and Ravenna in the year 2018, then find the income of Ravenna in the year 2017?
Rs. 1024
Rs. 1138
Rs. 2776
Rs. 2420
Rs. 4552
Solution :
Let the income of Asha in 2018 and 2017 be 3x and 5x respectively.
Let the income of Ravenna in 2018 and 2017 be 3y and 2y respectively
Since, the ratio of their income in the year 2017 was 5 : 4
5x : 2y = 5 : 4
2x = y
The sum of their incomes in 2018 is Rs. 10242
3x + 3y = 10, 242
9x = 10, 242
x = 1,138 and y = 2276
Ravenna’s income for the year 2017 = 2y = Rs. 4552
Hence, option E is correct.
HCF & LCM
The largest common factor of all the given numbers is known as the Highest Common Factor of the numbers.
The highest number that can be divided exactly into two or more numbers without any remainders.
It is also known as the Greatest Common Divisor (GCD)
The most easy way to find the HCF of two or more given numbers is to create a factor tree
How is HCF calculated?
Factorization Method
Prime Factorization Method
Division Method
The highest number that can be divided exactly into two or more numbers without any remainders.
It is also known as the Greatest Common Divisor (GCD)
The most easy way to find the HCF of two or more given numbers is to create a factor tree
How is HCF calculated?
Factorization Method
Prime Factorization Method
Division Method
HCF and LCM Questions for NRA CET 10th (Matriculate) Level:
Ex.
Find the least number which when divided by 48, 50, and 56, leaves the remainders 23, 25, and 31 respectively.
8375
5830
8600
7585
Solution :
Ex.
Find the least number which when divided by 48, 50, and 56, leaves the remainders 23, 25, and 31 respectively.
8375
5830
8600
7585
Solution :
48 – 23 = 25, 50 – 25 = 25, 56 – 31 = 25.
We see that in each case, the remainder is less than the divisor by 25.
The LCM of 48, 50 and 56 = 8400
Therefore, the required number 8400 – 25 = 8375
Hence, option (A) is correct.
HCF and LCM Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
A farmer has some number of cows and n number of cattle houses. He can tie 12 cows with equal number of cows in each cattle house or 8 cows with equal number of cows in each cattle house. What is the minimum possible number of cows the farmer has?
36
48
60
24
None of these
Solution :
Ex.
A farmer has some number of cows and n number of cattle houses. He can tie 12 cows with equal number of cows in each cattle house or 8 cows with equal number of cows in each cattle house. What is the minimum possible number of cows the farmer has?
36
48
60
24
None of these
Solution :
The minimum possible number of cows the farmer has = LCM of 8 and 12 = 24
Hence, option D is correct.
HCF and LCM Questions for NRA CET Graduate Level:
Ex.
There are 771 Girls and 1110 Boys in a school. Five boys and six girls are performing, rest of the boys and girls are made to sit on the ground in front of the stage in three groups at left, right and centre of the ground. The boys are divided in the left and right group in the ratio 2 : 3 and girls sit in the centre such that the number of columns in all three groups is same and maximum possible. Find the difference between the total number of rows of boys and girls.
13
15
20
4
None of these
Solution :
771 girls and 1110 boys
771 – 6 = 765 girls and 1110 – 5 = 1105 boys
1105 boys divided into ratio 2 : 3 → 442 boys and 663 boys
The maximum number of columns possible = HCF (765, 442, 663) = 17
| Number of rows of boys = | 1105 | = 65 |
| 17 |
| Number of rows of girls = | 761 | = 45 |
| 17 |
Difference = (65 – 45) = 20
Hence, option C is correct.
Trigonometry
It’s a branch of mathematics that deals with triangles, most right triangles. In particular the ratios and relationship between the triangles as sides and angles. It has two main ways of being used-
1. In Geometry
In its geometry application, it is mainly used to solve triangles usually right angle triangles. That is, given some angles and side lengths, we can find some or all the others.
2. Analytically
Its more advanced use, the trigonometric ratios such as Sine and Tangent, are used as functions in equations and are manipulated using algebra.
Trigonometry Questions for NRA CET 10th (Matriculate) Level:
Ex.
If P. cos θ + Q. sin θ = 8 and P. sin θ - Q. cos θ = 5, what is the value of (P2 + Q2)?
89
40
13
2√10
Solution :
1. In Geometry
In its geometry application, it is mainly used to solve triangles usually right angle triangles. That is, given some angles and side lengths, we can find some or all the others.
2. Analytically
Its more advanced use, the trigonometric ratios such as Sine and Tangent, are used as functions in equations and are manipulated using algebra.
Trigonometry Questions for NRA CET 10th (Matriculate) Level:
Ex.
If P. cos θ + Q. sin θ = 8 and P. sin θ - Q. cos θ = 5, what is the value of (P2 + Q2)?
89
40
13
2√10
Solution :
Given, P. cos θ + Q. sin θ = 8
⇒ P2. cos2 θ + Q2. sin2 θ + 2PQ. sin θ.cos θ = 64 ...... (i)
Also given, P. sin θ – Q. cos θ = 5
⇒ P2. sin2 θ + Q2. cos2 θ – 2PQ. sin θ.cos θ = 25 ......... (ii)
Adding equations (i) and (ii)
P2 + Q2 = 89
Option A, is hence the correct answer.
Area
It is a quantity that expresses the extent of a two dimensional region, shape. Area can be understood as the amount of material within a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It’s the two dimensional analogy of the length of a curve or the volume of solid. The area of a shape can be measured by comparing the shape to squares of a fixed size.
Area Questions for NRA CET 10th (Matriculate) Level:
Ex.
Perimeter of two squares of different areas is 40 cm and 24cm. Find the perimeter of a third square, whose area is equal to the difference of the area of these two squares.
30 cm
32 cm
35 cm
38 cm
Solution :
Ex.
Perimeter of two squares of different areas is 40 cm and 24cm. Find the perimeter of a third square, whose area is equal to the difference of the area of these two squares.
30 cm
32 cm
35 cm
38 cm
Solution :
Let the side of first square be x and the side of second square be y.
As, we have,
Perimeter of square = 4 × side
so, 4x = 40 & 4y = 24
⇒ 4x = 40 & 4y = 24
x = 10 cm & y = 6
Side of first square = 10 cm
Side of second square = 6 cm
Area of square ⇒ (Side)2
Area of first square ⇒ (10)2 = 100 cm2
Area of second square ⇒ (6)2 = 36 cm2
Area of third square ⇒ Area of first square – area of second square.
⇒ 100 – 36 ⇒ 64 cm2
Let the side of third square be z
So, Area of third square ⇒ (z)2
so,
z2 = 64
Hence, z = 8
So, the side of third square = 8 cm
therefore the perimeter of the third square ⇒ 4 × side
⇒ 4 × 8 = 32 cm
Hence, optiion (B) is correct.
Area Questions for NRA CET 12th (Higher Secondary) Level:
Ex.
The area of a square is equal to the area of a rectangle of length 28 cm and breadth 7 cm. Find the circumference of the circle whose diameter is equal to the side of the square.
110 cm
44 cm
66 cm
88 cm
None of these
Solution :
Area of square = (side)2
And, Area of rectangle = 28 × 7 = 196 cm2
Now,
(side)2 = 196 cm2
∴ side of square = 14 cm
Then, Radius of circle
| = | side of square | = | 14 | = 7cm |
| 2 | 2 |
⇒ Radius of circle = 7cm
We know that,
Circumference of circle = 2 π (Radius)
| = 2 × | 22 | × 7 |
| 7 |
= 44 cm
Hence, option (B) is correct.
Area Questions for NRA CET Graduate Level:
Ex.
If the length of a rectangle is increased by 25% and the breadth is reduced by 33.33% then what will be the effect on its diagonal(approximately)?
7.6%
8.33%
6%
7.33%
None of these
Solution :
Let the length of the rectangle = 4 units
And breadth of the rectangle = 3 units
Then diagonal of the rectangle = √(42 + 32) = 5 units
According to the question, the length of a rectangle is increased by 25% and the breadth is reduced by 33.33%
New length = 125% of 4 units = 5 units
New breadth = 66.66% of 3 units = 2 units
In the new rectangle, New diagonal= √(52 + 22) = √29 = approximately 5.38 units
| Change = (5.38 – 5) × | 100 | = 7.6% |
| 5 |
Hence, option A is correct.
NRA CET Mock Test
Due to great demand for the government posts Jobs the level has become difficult. And thus the overall process is tightened to get the best. Aspirants have to give their Best to crack the exam. Hence to overcome all such hurdles a good strategy is required to guide you through all. The study material will help you in pre preparation for the Exam.


